製品例詳細情報
ペンタゴナルシェルフの平面展開のシミュレーション(その1)においては、今回は15世紀ルネサンス期のドイツの画家である Albrecht Dürer(アルブレヒト・デューラー)の平面充填 [*]のひとつを紹介しました。
ここでは Albrecht Dürer(アルブレヒト・デューラー)の平面充填の別のひとつをご紹介いたします。
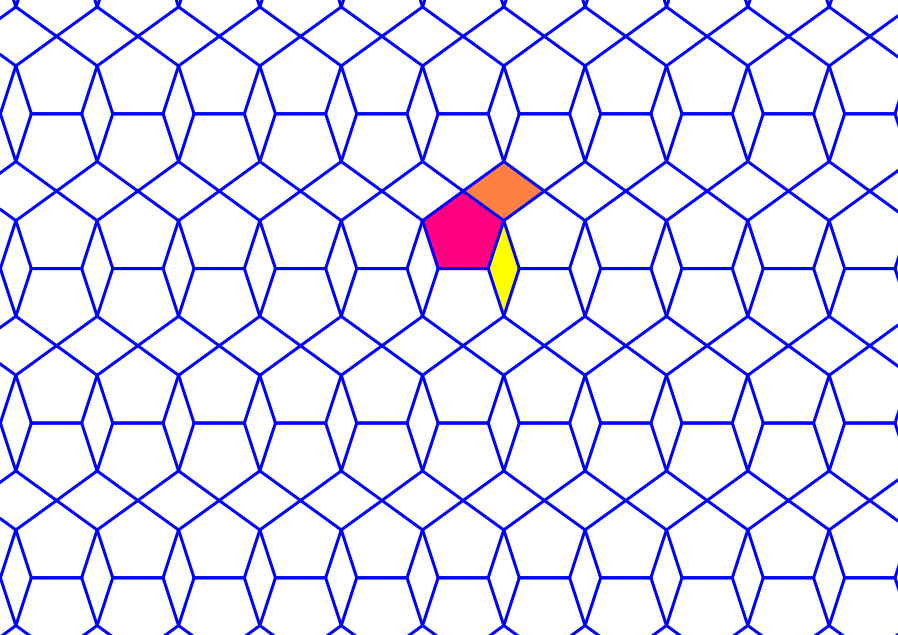
Figure 1 をご覧ください。
これは正五角形 (pentagon :シアン) と2種類の菱形 (rhombus :イェロウとオレンジ) の合計3種類の平面図形を用いた平面充填で、Dürer's thick tiling と呼ばれています。
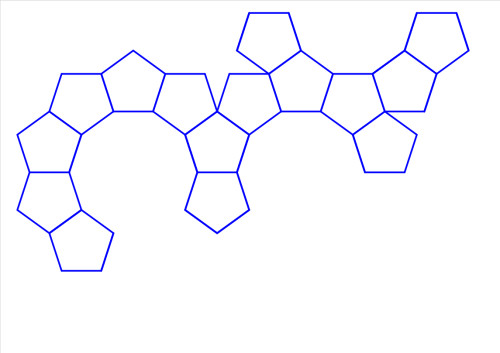
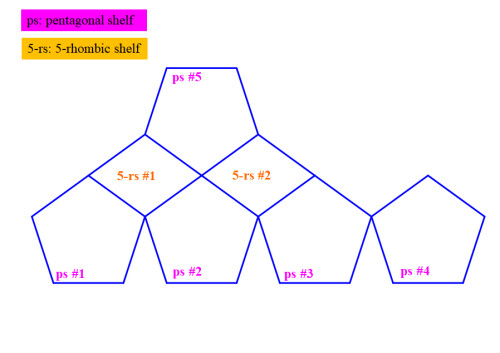
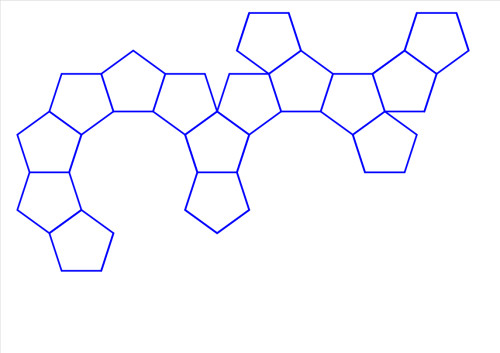
これを参照して5個のペンタゴナルシェルフを連結したのが Figure 2 です。
ペンタゴナルシェルフの平面展開のシミュレーション(その1)の場合は菱形シェルフを挟まなくともペンタゴナルシェルフだけでウォールに安定させ固定できますが、この場合は2種類の菱形のいっぽうであるオレンジの菱形シェルフを挟まないとウォールに安定させて固定が困難となります。
Figure 1 Dürer's thick tiling
Figure 2 5個のペンタゴナルシェルフと2個の菱形シェルフの連結
ペンタゴナルシェルフの平面展開のシミュレーション(その3) では、天文学上に偉大な足跡を残したKeplerの平面充填に関して述べます。
彼の書籍 Harmonice Mundi では、幾何学、建築、調和、形而上学、心理学、占星術、天文学からなる宇宙全般に関しての考えを記載しています。
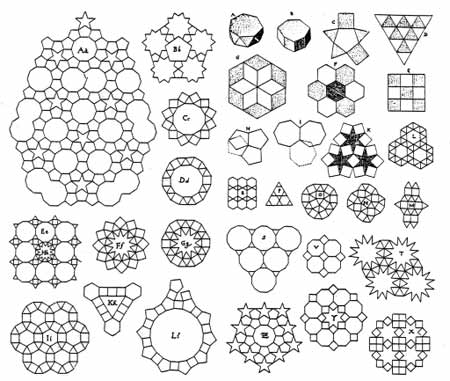
その著作の中に、Photo 1 に示すように Kepler が Aa と表示した図例があります。
Photo. 1 の左最上段の図例が Kepler's Aa です。
Figure 1 は Kepler's Aa を再現したものです。
Kepler's Aaは、下記の異なる4種類の要素平面図形から構成されています。
Figure 1 KeplerのAa:4種類の異なる要素平面図形から構成されています。
Figure 3 15個のペンタゴナルシェルフの連結シミュレーション
なおこの事項に関しての詳細は、下記の MyBlog をご訪問ください。